Введение
Развитие методов цифровой передачи и обработки данных в значительной степени определяется возможностями систем обеспечения высокой достоверности передаваемой информации. Наиболее эффективным средством повышения достоверности цифровой информации является применение помехоустойчивого кодирования. Обзор наиболее перспективных методов кодирования по критерию «эффективность-производительность» был сделан в [1], где указывалось, что наибольшее предпочтение в высокоскоростных каналах спутниковой связи заслуживают многопороговые декодеры (МПД) [2].
В большинстве последних публикаций по МПД представлены результаты его исследования в каналах передачи данных с двоичной фазовой модуляцией (ФМ2). В таких условиях при сопоставимой эффективности МПД оказывается существенно (на два-три порядка) проще для реализации, чем другие методы коррекции ошибок [3]. Вместе с тем в современных телекоммуникационных системах на каналы передачи данных часто накладываются значительные ограничения по занимаемой полос частот и с каждым годом эти ограничения становятся все жестче. Одним из способов уменьшения занимаемой полосы частот является использование многопозиционных сигналов, для формирования которых обычно применяется многопозиционная фазовая (ФМN) или квадратурная амплитудная модуляция (КАМN). В таких условиях для улучшения энергетики канала также необходимо применять помехоустойчивые коды. Можно предположитьчто МПД, обладающие большой корректирующей способностью в каналах с двоичной фазовой модуляцией, будут обладать такой же высокой эффективностью и в каналах с многопозиционными сигналами. Таким образом, целью данной работы является применение многопороговых декодеров в каналах с многопозиционной модуляцией и исследование их эффективности в таких условиях. 1. Применение МПД с многопозиционными системами сигналов
При использовании высокоэнергетичных сигналов и жестких требованиях к ширине полосы частот высокие значения эффективности возможны в случае совместного применения многопозиционных систем модуляции и кодирования. Принципы использования МПД для систем сигналов на плоскости типа КАМN и ФМN также разработаны уже достаточно давно [4]. Это позволяет считать, что возможность применения МПД с этими типами сигналов в настоящее время также вполне очевидна. При переходе к многомерным сигналам все подходы к применению МПД совместно с такими сигнальными конструкциями остаются аналогичными двумерному случаю, что позволяет одновременно получить значительный энергетический выигрыш кодирования и существенно сэкономить полосу частот передаваемого сигнала.
Рассмотрим принцип многопорогового декодирования для такой системы сигналов на примере КАМ16, для которой расположение сигнальных точек показано на рис. 1. 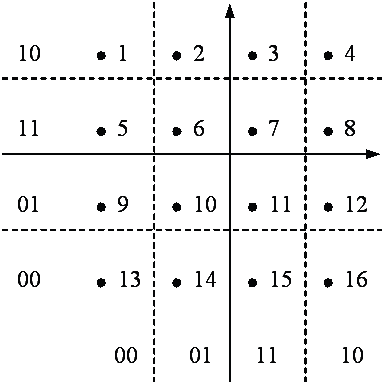 Рис. 1. Двумерная система сигналов для КАМ16 Двоичные пары битов на горизонталях и вертикалях дают представление об одном из вариантов соответствия между сигнальными точками и четверками битов, которые поступают в модем передатчика от кодера, а затем приходят из демодулятора в декодер приемника. Существенным для обеспечения достаточно хорошего согласования систем модуляции и кодирования является то, что для каждого данного сигнала соседние с ним по горизонтали и вертикали сигналы отличаются только в одном бите, а те, которые находятся на диагонали – в двух битах. Такое установление соответствия между сигнальными точками и четверками битов называется кодированием двумерным кодом Грея. На самом деле можно проверить, что свойство увеличения веса Хемминга разности двоичных представлений сигнальных точек имеет место при удалении от любого исходного сигнала не только на 1, но и на 2 позиции, причем соответствующие логарифмы отношений вероятностей для случая удвоения веса Хемминга также примерно удваиваются. Это позволяет считать двоичные векторы разностного и синдромного регистров МПД [2], как и в случае обычной ФМ2, эффективной мерой разности расстояний между передаваемыми символами такой недвоичной системы передачи. Аналогичные свойства справедливы и при росте числа сигнальных точек в рамках прямоугольной системы сигналов на плоскости или в пространствах большей размерности.
Таким же образом организуется соответствие между сигналами и их двоичным представлением в случае многопозиционной круговой системы сигналов, например, фазовой манипуляции вида ФМN. Для примера на рис. 2 показано расположение сигнальных точек для системы сигналов ФМ8. Легко видеть, что в случае ФМN имеет место рост веса Хемминга для разности двоичных представлений между всеми соседними или удаленными друг от друга на две позиции сигнальными точками. Рис. 2. Двумерная система сигналов для ФМ8 Но из такого монотонного увеличения веса разности двоичного представления сигналов по мере их удаления от любого передаваемого символа в системе КАМN или ФМN получаем, что и в случае жесткого модема, и при использовании мягкого модема рост весов и сумм проверок на пороговых элементах с хорошей точностью пропорционален логарифму отношения вероятностей текущего решения МПД и того удаленного потенциального нового решения, для которого и вычисляется сумма проверок двоичного кода со специально подобранными кодовыми полиномами для системы многопозиционной модуляции. Именно в этом случае суммы проверок соответствуют сравнению кодовых слов, у которых нет различий в том, рассматриваются ли разности в битах внутри передаваемых символов или все различия наблюдаются только между некоторыми битами в различных символах. Такое устранение различий между двоичными представлениями соотношения расстояний в векторах синдромного и разностного регистров при использовании кода Грея позволяет успешно применять двоичные МПД со сложными системами сигналов. 2. Эффективность МПД в каналах с многопозиционными системами сигналов
В данном разделе представлены результаты моделирования МПД и других методов коррекции ошибок в канале с многопозоционными системами сигналов. При моделировании использовалась модель канала, задаваемая выражением 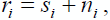 где 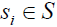 – передаваемый комплексный сигнал; S – множество возможных сигналов, определяемое выбранной системой модуляции; r i – принятый комплексный сигнал; n i – комплексный аддитивный белый гауссовский шум со спектральной плотностью мощности N 0/2 в каждой размерности.
Заметим, что все представленные далее результаты получены для случая использования жесткого модема, когда демодулятор не формирует оценок надежности своих решений для принятых битов.
Для получения таких решений использовался демодулятор по максимуму правдоподобия, выполняющий оценку переданного символа по формуле 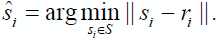 На рис. 3 кривыми 1 – 3 представлены экспериментальные графики зависимости вероятности ошибки на бит Pb(e) на выходе многопорогового декодера от отношения сигнал-шум Eb/N0 в канале связи с аддитивным белым гауссовским шумом (АБГШ) и квадратурной амплитудной модуляцией при использовании 16, 32 и 64 символьных созвездий. При декодировании выполнялось от 10 до 15 итераций декодирования блокового самоортогонального кода с кодовой скоростью R = 1/2, кодовым расстоянием d = 9 и длиной n порядка 10000. Рис. 3. Эффективность МПД в каналах с КАМN На рис. 3 кривыми 4 и 5 также представлены характеристики декодера Витерби [5] для кода с длиной регистра K = 7 при использовании КАМ16 и КАМ32 соответственно. Как видно, декодер Витерби в данных условиях при Pb(e) = 10–4 проигрывает МПД примерно 2 и 3 дБ. Кривыми 6 и 7 на рис. 3 также показаны характеристики очень мощного турбо кода [6] с кодовой скоростью R = 1/2, который образован путем параллельного каскадирования двух рекурсивных систематических сверточных кодов с конструктивной длиной K = 4. В данном турбо коде применялся перемежитель типа S-random длиной L = 5000 (общая длина турбо кода составляет n = 10000). При декодировании турбо кода выполнялось 8 итераций, на каждой из которых для декодирования составляющих кодов применялся Max-Log-MAP алгоритм. Из сравнения характеристик турбо кода и МПД видно, что эффективность последнего оказывается хуже примерно на 1..2 дБ, но МПД при этом почти на два порядка проще для практической реализации, чем данный турбо код [3]. Рис. 4. Эффективность МПД в каналах с ФМN На следующем рис. 4 представлены характеристики МПД для того же блокового кода, что и на рис. 3, в канале с многопозиционной фазовой модуляцией (ФМN). При этом использовалась такая же модель канала с другим множеством сигнальных точек S .
Видно, что соотношения между характеристиками многопорогового декодера, декодера Витерби и турбо кода сохраняются и при данном виде модуляции.
Заключение
Таким образом, рассмотрены вопросы применения многопороговых методов декодирования в каналах с многопозиционными системами модуляции, таких как квадратурная амплитудная и многопозиционная фазовая модуляция. Показано, что в данных условиях МПД является на 2..3 дБ более эффективным, чем классический декодер Витерби, и уступает декодеру турбо кода около 1..2 дБ. При этом сложность практической реализации МПД оказывается на два или даже более порядков меньше сложности декодера турбо кода и других методов коррекции ошибок с сопоставимой эффективностью. Это допускает применение многопороговых декодеров в высокоскоростных системах передачи данных, в которых наряду с высокими требованиями к энергетике канала накладываются жесткие ограничения на расширение полосы частот.
Дополнительную информацию о МПД можно найти на веб-сайте [7].
Библиографический список
1. Золотарев В.В., Овечкин Г.В. Эффективные алгоритмы помехоустойчивого кодирования для цифровых систем связи // Электросвязь. 2003. №9. С. 34–37.
2. Золотарев В.В., Овечкин Г.В. Помехоустойчивое кодирование. Методы и алгоритмы. Справочник. М.: Горячая линия – Телеком, 2004. 126 с. 3. Золотарев В.В., Овечкин Г.В. Сложность реализации эффективных методов декодирования помехоустойчивых кодов // 6-я межд. конф. и выст. «Цифровая обработка сигналов и ее применение». М.: 2004. Том 1. С. 220–221. 4. Банкет В.Л., Золотарев В.В. Эффективность многопозиционных систем модуляции и многопорогового декодирования // В сб.: ЕС Всесоюзная школа семинар по вычислительным сетям». М.-Пушкино, 1984. Ч.3.2. 5. Витерби А. Границы ошибок для сверточных кодов и асимптотически оптимальный алгоритм декодирования // Некоторые вопросы теории кодирования. М.: Мир, 1970. С. 142–165. 6. Berrou C., Glavieux A., Thitimajshima P. Near Shannon Limit Error-Correcting Coding and Decoding: Turbo Codes // Proc. of the Intern. Conf. on Commun. (Geneva, Switzerland). 1993. May. P. 1064–1070. 7. Веб-сайт www.mtdbest.iki.rssi.ru. |