Автор: Степанов А. В., Матвеев С. А.
"Методы компьютерной обработки сигналов систем радиосвязи"
Все права в отношении данного документа принадлежат автору. Характерной особенностью современных систем и сетей связи является использование различных методов адаптации, в результате применения которых в каналах связи по различным причинам могут изменяться вид модуляции и параметры используемых сигналов в течение одного и того же сеанса связи. Наиболее показательным примером является изменение скорости передачи формации в зависимости от качества каналов связи. Однако встречаются и более сложные методы адаптации. Кроме того, в условиях неполных априорных сведений о параметрах принимаемого сигнала решение ряда задач его обработки, таких как установка полос основной селекции приемника, настройка демодулятора, принятие демодулятором правильного решения о переданеом значении модуляционного параметра, требует возможно более точного знания модуляционной структуры поступающего из эфира сигнала. Эти факторы обусловливают необходимость включения в тракты обработки средств автоматического определения параметров и видов модуляции принимаемых сигналов. Определение априорно неизвестных модуляционных параметров широкого класса принимаемых сигналов в общем случае является сложной задачей, требующей значительных вычислительных ресурсов. Это создает трудности при реализации автоматических процедур распознавания вида и параметров модуляции, работающих в реальном масштабе времени. Однако в ряде случаев, рассмотренных в настоящем разделе, реализация таких процедур возможна путем применения соответствующих математических методов и современных средств вычислительной техники. Решение задачи вскрытия модуляционной структуры сигнала предполагает определение совокупности признаков, характеризующих требуемые виды модуляции и их параметры, выделение, данной совокупности признаков из принимаемой смеси сигнала и помех и обработку признаков с целью принятия решения о модуляционных параметрах анализируемого сигнала. Общая схема работы подсистемы анализа представлена на рис. 3.3.1. 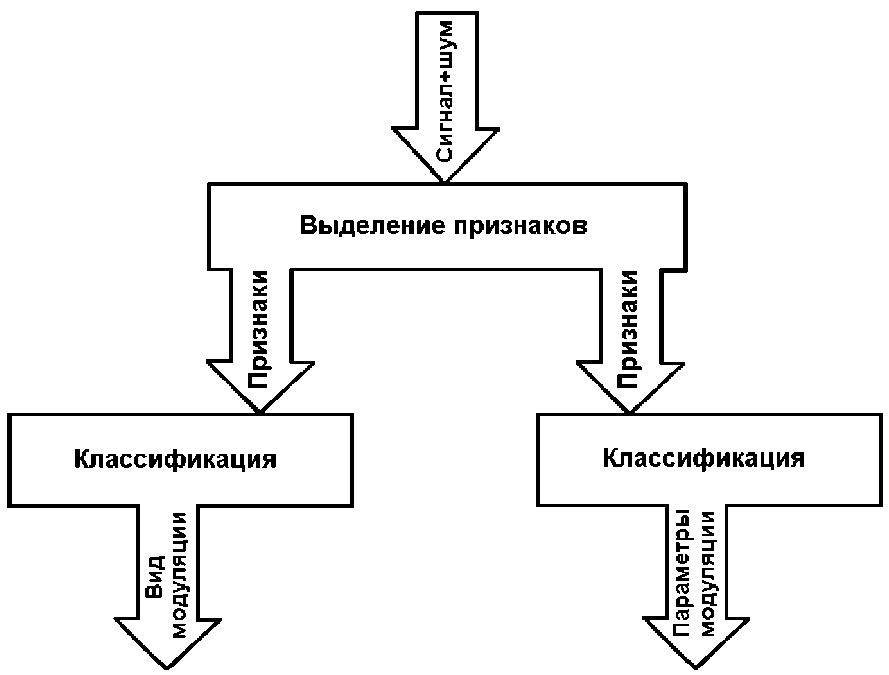
Рис. 3.3.1 Постановка проблемы определения модуляционной структуры сигнала с точки зрения общей теории оптимального приема может быть сформулирована следующим образом. На заданном временном интервале наблюдается сигнал x(t) = s(t, q1, q2, ... , qn) + N(t), где q1, q2, qn - оцениваемые параметры модуляционной структуры, N(t) - шум канала приема. Необходимо принять решение о приеме сигнала с i-м вариантом модуляционной структуры, если априорно известно, что - множество значений, которые может принимать i-й параметр. - множество значений, которые может принимать i-й параметр. При равномерности распределения значений q1, q2, ..., qn коэффициент правдоподобия может быть выражен в следующей форме [33] 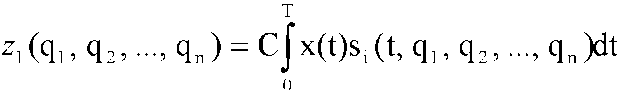
где C - некоторая константа. Максимально правдоподобное решение о наличии в реализации i-го сигнала принимается, если для всех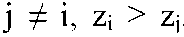 . Практическая реализация данного решающего правила приведет к необходимости построения корреляционного приемника, содержащего L каналов корреляции, в каждом из которых определяется корреляционный интеграл входной смеси x(t) с i-м сигналом si, i = 1, ..., L. В условиях контроля сигналов современных систем цифровой связи трудно ограничить величину L одним приемлемым значением вследствие непрерывности значений параметров qi для анализируемых сигналов (так, например, скорость манипуляции для сигналов, занимающих полосу стандартного телефонного канала, в общем случае может принимать любое значение в диапазоне 1...2400 Бод). Данный факт делает невозможным применение классических методов оптимальной оценки параметров вследствие недопустимо больших вычислительных затрат при реализации данных методов. . Практическая реализация данного решающего правила приведет к необходимости построения корреляционного приемника, содержащего L каналов корреляции, в каждом из которых определяется корреляционный интеграл входной смеси x(t) с i-м сигналом si, i = 1, ..., L. В условиях контроля сигналов современных систем цифровой связи трудно ограничить величину L одним приемлемым значением вследствие непрерывности значений параметров qi для анализируемых сигналов (так, например, скорость манипуляции для сигналов, занимающих полосу стандартного телефонного канала, в общем случае может принимать любое значение в диапазоне 1...2400 Бод). Данный факт делает невозможным применение классических методов оптимальной оценки параметров вследствие недопустимо больших вычислительных затрат при реализации данных методов. Другим вариантом решения задачи определения модуляционной структуры сигнала является использование методов статистической теории распознавания образов. Постановка задачи распознавания предполагает выбор признаков распознавания, определение их статистических характеристик, формирование эталонных описаний распознаваемых классов, выбор решающего правила отнесения контрольной выборки и способов оценивания ошибок распознавания. В классической постановке задача распознавания формулируется как задача отнесения некоторой контрольной выборки признаков распознавания {xi}, i = 1, ..., N к одному из распознаваемых классов Si, ..., Sm.При этом известные методы распознавания отличаются в основном способами описания S1, ..., Sm. В настоящее время хорошо изучена задача распознавания для полностью описанных классов, когда они однозначно определяются функциями распределения Wi(x) = W(x|Si), либо функциями плотности вероятности w(x|Si) = dW(x|Si)/dx и априорными вероятностями их появления pi. В [34] показано, что при проверке простой гипотезы против простой альтернативы (то есть при m = 2) наиболее широко используемые критерии принятия решения (Байесовский, Неймана-Пирсона, минимаксный, максимума апостериорной вероятности и др.) основаны на сравнении отношения правдоподобия с некоторым заранее выбранным порогом. Отношением правдоподобия называется функция 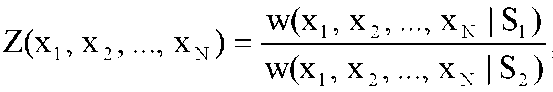 1 1
где x1, x2, ..., xN - контрольная выборка. В случае некоррелированной контрольной выборки 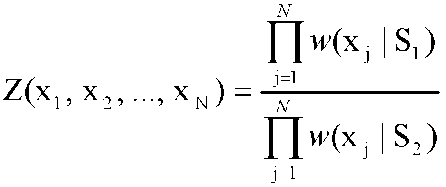
При сравнении отношения правдоподобия с порогом, равным 1, критерий называется критерием максимума правдоподобия. В эквивалентной форме решающее правило выглядит следующим образом. Принимается гипотеза S1 если 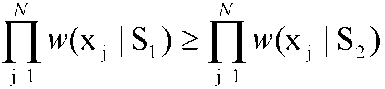 (3.3.1) (3.3.1)
и S2 в противном случае. В ряде случаев для того, чтобы перейти от мультипликативного критерия приятия решения к аддитивному, используется логарифм отношения правдоподобия. В этом случае решающее правило приводится к виду 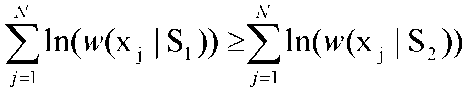
Нетрудно видеть, что данные процедуры распознавания верны и в случае, если признаки распознавания являются векторами некоторых случайных величин, то есть в многомерном случае. В случае, когда функции распределения известны с точностью до вектора параметров, разработаны методы, основанные на восстановлении функций распределения классов путем статистического оценивания параметров их законов распределения. В этих случаях наиболее часто используемыми параметрами являются математическое описание и дисперсия, несмещенные оценки которых равны 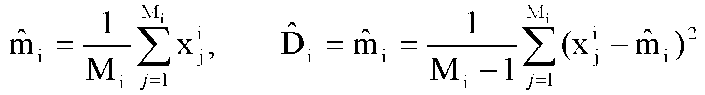 , (3.3.2.) , (3.3.2.)
где {xij}, j = 1, ..., Mi - обучающая выборка класса Si. Если же вид функций W(x|Si) неизвестен, применяются методы распознавания, включающие вычисление статистических оценок функций распределения Ŵ(x|Si) или функций плотности вероятности ŵ(x|Si) по обучающим выборкам, которые впоследствии используются в процедурах распознавания. В настоящее время разработано большое количество методов вычисления оценок ŵ(x|Si) по выборкам конечного объема. Рассмотрим основные из них. Часто используемым способом является построение гистограммы. Для этого пространство признаков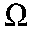 разбивается на n непересекающихся подмножеств разбивается на n непересекающихся подмножеств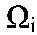 , таких, что , таких, что 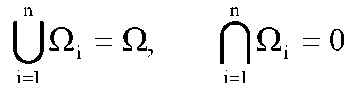
Пусть {xij}, j = 1, ..., Mi - обучающая выборка класса Si. После этого подсчитывается относительное количество попадания значений {xij}, j = 1, ..., Mi в области 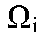 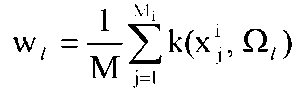
где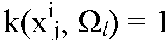 , если , если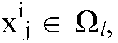 и и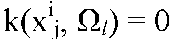 в противном случае. в противном случае. При таком способе построения оценки существует несколько проблем. Основной из них является выбор способа разбиения множества признаков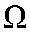 на подмножества на подмножества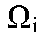 . Слишком мелкое разбиение влечет за собой возникновение «пустых» интервалов, а сокращение количества подмножеств . Слишком мелкое разбиение влечет за собой возникновение «пустых» интервалов, а сокращение количества подмножеств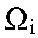 заведомо огрубляет оценку функции плотности вероятности. Кроме того, оценка в виде гистограммы при фиксированном разбиении и объеме обучающей выборки, стремящейся к бесконечности, сходится к функции заведомо огрубляет оценку функции плотности вероятности. Кроме того, оценка в виде гистограммы при фиксированном разбиении и объеме обучающей выборки, стремящейся к бесконечности, сходится к функции 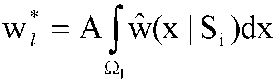 5 5
которая отличается от действительной функции плотности вероятности.Значительное место в литературе по статистическому оцениванию занимает метод k-го ближайшего соседа. Пусть km - заранее заданное число, меньшее или равное объему выборки Mi и p(x, xi1, xi2, ..., xiMi) - расстояние от k-й ближайшей точки выборки {xij}, j = 1, ..., Mi до x. Тогда оценка для плотности вероятности выражается как 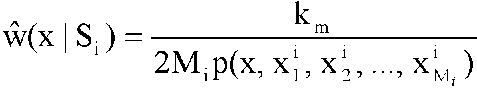 . (3.3.4.) . (3.3.4.)
В данной оценке неопределенным является выбор параметра km.При решении практических задач часто выбирают 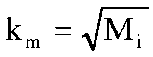
В [35] рассмотрена оценка функции плотности вероятности виде 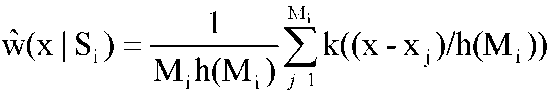 , (3.3.5.) , (3.3.5.)
где функция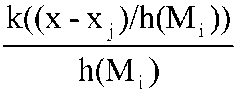 называется ядром оценки. называется ядром оценки. Данная оценка, известная как оценка Парзена, имеет множество модификаций в зависимости от вида ядра. В одномерном случае при выполнении условия к((х - хj)/h(Мi)) = 1/2 для |h(Mi)| ≤ 1 и k((x-xj)/h(Mi)) = 0 для |h(Mi)| > 1 оценка называется оценкой Парзена-Розенблатта. Возможно вычисление оценки ŵ(x|Si) следующим образом. На первом этапе производится вычисление оценки функции распределения Ŵ(x|Si), на втором производится преобразование Ŵ(x|Si) → ŵ(x|Si). Пусть {xij} j = 1, ..., М, - обучающая выборка класса Si. В этом случае в качестве оценки Ŵ(x|Si) может быть выбрана функция 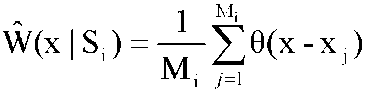
где θ(х - хj) = 1, если х - хj ≥ 0, и θ(х - хj) = 0 в противном случае. Оценка ŵ(x|Si) в этом случае вычисляется за счет приближения ступенчатой функции Ŵ(x|Si) линейной функцией, коэффициенты которой определяются по методу наименьших квадратов в точках хк = х + kh, k = -k0, -k0 + 1, ..., 0, ..., k0 - 1, k0, где k0 — количество шагов аппроксимации. В этом случае 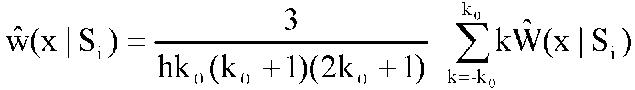 (3.3.6) (3.3.6)
Следует отметить, что оценка Парзена-Розенблатта является частным случаем полученной оценки при k0 = 1. Подставляя в полученную формулу выражение для Ŵ(x|Si), получим 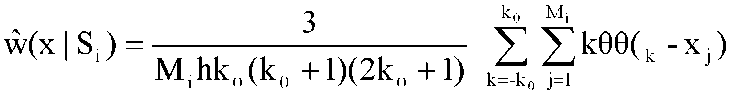
В качестве эталонных описаний распознаваемых классов могут быть использованы и непосредственные значения обучающих выборок {xij} j = 1, ..., М. В этом случае применяются ранговые критерии распознавания, суть которых состоит в следующем. Обучающие выборки для каждого из классов и контрольная выборка «перемешиваются», после чего упорядочиваются по возрастанию или убыванию. Для каждого из классов вычисляется функция, характеризующая степень перемешивания, по максимуму которой и принимается решение о принадлежности контрольной выборки к какому-либо из классов. Рассмотрим некоторые практические вопросы распознавания вида и модуляционных параметров ряда разновидностей сигналов с частотной и фазовой манипуляцией. С точки зрения вскрытия модуляционной структуры вся значащая информация о таких сигналах содержится в их фазовых и частотных параметрах. Иначе говоря, она содержится в значениях мгновенной частоты f(nT) и фазы р(nТ) сигнала. Мгновенная амплитуда а(nТ) при анализе модуляционных параметров ЧМ- и ФМ-сигналов в общем случае не является информационным параметром, хотя учет ее значений в алгоритмах частотного и фазового детектирования позволяет компенсировать замирания принимаемого сигнала. Для определения вида и параметров модуляции ЧМ- и ФМ-сигналов необходимо оценивать мгновенную угловую фазу сигнала, которая может быть представлена в виде p(nT) = 2πf0 + 2πf(nT) + p0(nT), где f0 - центральная частота сигнала, параметры f(nT) и р0(nТ) — соответственно мгновенная частота и мгновенная начальная фаза сигнала. Данные параметры могут, например, принимать следующие значения • для ЧМ-сигналов без скачка фазы f(nT) = (i - М)Δf + Δf/2, р0(nТ) = const; • для ФМ-сигналов р0(nТ) = (2π(I - М)/М)nТ, f(nT) = 0, где i = 1,..., М, М - число позиций модуляции, Δf - разнос частот. Представление мгновенной фазы сигнала в форме 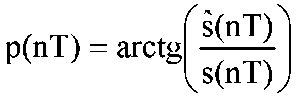
ограничивает ее главное значение в диапазоне [-π/2...π/2]. Поскольку более важная с точки зрения параметров модуляции информация заключается не в абсолютном значении мгновенной фазы, а в ее скачках, то для дальнейшего анализа целесообразно использовать приведенные разности отсчетов мгновенной фазы Δp(nT) = p(nT) - p((n - l)T) , если Δp(nT) ≥ 0 , и
Δp(nT) = p(nT) - p((n - l)T) + 2π в противном случае. То есть, для удобства дальнейшей обработки отрицательные скачки разности фаз приводятся к диапазону [0...2π]. Конкретное значение индекса l устанавливается с учетом возможного значения максимальной скорости Vmax анализируемого сигнала таким образом, чтобы обеспечить выполнение соотношения l/Vmax ≈ l Т. Расположение пиков полученной гистограммы разности фаз, отстоящих на определенном расстоянии друг от друга, зависит от наличия и значений постоянного скачка фазы анализируемого сигнала и позволяет принимать решение об используемом виде модуляции и числе ее позиций. Данный факт иллюстрируется на рис. 3.3.2, а и б, где приведены вычисленные гистограммы разности фаз ФМ2- и ФМ4-сигналов при соотношении сигнал шум 3/1. 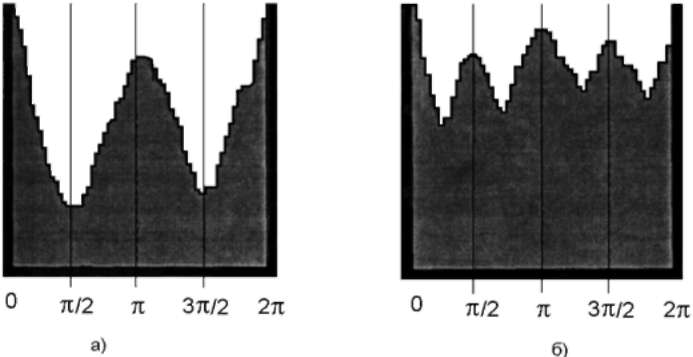
Рис.3.3.2. Для ЧМ- и ФМ-сигналов на интервале одной посылки значение разности фаз Δр(nТ) должно быть близко к 0. При этом значений, близких к 0, должно быть достаточно много, так как время переходного процесса при смене частотных позиций для широкого класса сигналов не превышает 10% от длительности элементарной посылки. При смене частотных позиций при приеме ЧМ-сигналов с разрывом фазы возможные значения Δр(nТ) в общем случае будут случайными и их распределение можно принять равномерным в интервале [0...2π]. Значения разности фаз при приеме ЧМ-сигналов без разрыва фазы в случае смены частотных позиций будут близки к 0. Очевидно, что для ФМ-сигналов при изменении значения модуляционного параметра наибольшие значения пиков функции плотности вероятности значений Δр(nТ) будут приходиться на значения 0, π/2, π, Зπ/2 (за исключением сигналов ФМ4 со сдвигом на π/4). Таким образом, существуют реальные физические предпосылки для использования при распознавании ЧМ- и ФМ-сигналов значений разности фаз Δр(nТ) в качестве признаков распознавания. Ввиду того, что функции плотности вероятности для классов SЧМ и SФМ, в особенности при неизвестных законах распределения шумов в канале связи, не описываются стандартными формулами, единственно возможным способом является вычисление статистических оценок ŵ(x|SЧМ) и ŵ(x|SФМ) с последующим принятием решения в соответствии с критерием (3.3.1). Однако эксперименты на реальных и смоделированных на ЭВМ сигналах показывают, что вероятность правильного распознавания в данном случае превышает 0,7 при вероятности ошибки второго рода 0,3. При этом для области изменения величины Δр(nТ) от 0 до 2л способ оценки функций плотности вероятности (3.3.3) - (3.3.6) на вероятности ошибок первого и второго рода влияет незначительно. Низкая достоверность распознавания в сочетании со сравнительно большими затратами вычислительных ресурсов не позволяет использовать данный непараметрический метод распознавания в трактах обработки сигналов для определения параметров и вида модуляции ЧМ- и ФМ-сигналов. Причиной недостатков описанного метода распознавания является низкая информативность выбранного признака распознавания, так как значения Δр(nТ) вблизи 0 для обоих распознаваемых классов составляют от 50 до 80% измеряемых значений и, как следствие, являются малоинформативными. Выбор более информативных признаков связан с исследованием особенностей поведения случайного процесса Δр(nТ) и вычислением его параметров, таких как выбросы случайного процесса. Параметром, наиболее полно отражающим различия распознаваемых совокупностей, является величина x = τ1/τ0, где τ0 - время пребывания случайного процесса Δр(nТ) в интервале [π/4—7π/4], τ1 - время пребывания случайного процесса Δр(nТ) в интервалах [Зπ/8, 5π/8|, [7π/8, 9π/8], [11π/8, 13π/8]. Для рассматриваемого дискретного случая 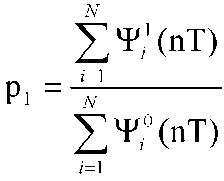 (3.3.7) (3.3.7)
где ψ1i (nT) = 1, если Δр(nТ) ∈ [Зπ/8, 5π/8] ∪ [7π/8, 9π/8] ∪ [11π/8, 13π/8] и ψ1i (nT) = 0 в противном случае, ψ0i (nT) = 1, если Δр(nТ) ∈ [π/4, 7π/4| и ψ0i (nT) = 0 в противном случае. Если в процессе вычисления величины x накопление данных проводить до тех пор, пока знаменатель выражения (3.3.7) не достигнет некоторого фиксированного значения N , выражение (3.3.7) преобразуется к виду 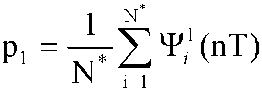 , (3.3.8) , (3.3.8)
Полученное выражение является статистической оценкой вероятности пребывания случайного процесса Δр*(nТ) в области [Зπ/8, 5π/8|, [7π/8, 9π/8], [11π/8, 13π/8]. Случайный процесс Δр*(nТ) получается за счет удаления из процесса Δр(nТ) значений, лежащих в интервалах от 0 до π/4 и от 7π/4 до 2π. В силу центральной предельной теоремы величина (3.3.8) распределена по нормальному закону. Таким образом, задача распознавания классов SЧM и SФМ сводится к стандартной задаче распознавания двух совокупностей, распределенных по нормальному закону с разными математическими ожиданиями и дисперсиями. В этом случае решающее правило распознавания сигналов с ЧМ и ФМ можно представить в виде p1 > 0.75 - принимается гипотеза SФМ, (3 3 9) p1 ≤ 0.75 - принимается гипотеза SЧМ. Аналогичная процедура распознавания может быть использована при распознавании сигналов ФМ2 и ФМ4. В этом случае выражение 3.3.8 преобразуется к виду 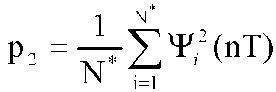 , (3.3.10) , (3.3.10)
где ψ1i (nT) = 1, если Δр(nТ) ∈ [Зπ/4, 5π/4], и ψ2i (nT) = 0 в противном случае. Решающее правило при этом выглядит следующим образом p2 ≥ 0.66667 - принимается гипотеза SФМ2, (3 3 11) р2 < 0.66667 - принимается гипотеза SФМ4. Количественно оценить вероятность правильности определения вида модуляции по решающему правилу (3.3.9) можно следующим образом. Теоретическая потенциально достижимая вероятность ошибки различения двух сигналов (в нашем случае ЧМ- и ФМ-сигналов) по одному признаку, распределенному по нормальному закону, при воздействии гауссовых шумов и без учета погрешностей самого измерителя признака определяется в следующем виде [36] 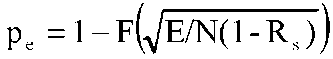
где F() - интеграл вероятности, E/N - отношение энергии сигнала к энергии шума, Rs — коэффициент взаимной корреляции сигналов по оцениваемому параметру. Благодаря известной математической зависимости между фазой и частотой, любое изменение мгновенной частоты будет приводить к изменению мгновенной фазы (и наоборот). Теоретический коэффициент корреляции между оценками данных параметров Rs = 0,87 [36]. Потери в точности измерения параметров сигнала при дискретной обработке методом накопления и усреднения оценок при номинале частоты дискретизации, удовлетворяющим требованию теоремы Котельникова, и числе уровней квантования, перекрывающим динамический диапазон изменения уровня сигнала, асимптотически стремятся к нулю [36]. Таким образом, можно получить количественную оценку ожидаемой потенциальной вероятности ошибки определения вида модуляции на основе контроля фазовых параметров: ре ≈ 0,2 при E/N = 2, ре ≈ 0,025 при E/N = 4, ре ≈ 0,003 при E/N = 8. Результаты экспериментальной проверки предлагаемого метода распознавания на реальных и моделируемых ФМ- и ЧМ-сигналах при объеме выборки N = 4096 показали ухудшение (в среднем на 2 дБ по помехоустойчивости) вероятности правильного решения по правилу (3.3.9) по сравнению с теоретическими потенциально возможными значениями в области относительно низких значений отношения сигнал/шум 1... 8 дБ. Повышение эффективности процедуры распознавания связано с увеличением объемов обучающих и контрольных выборок. В ряде случаев целесообразно использование модифицированного правила (3.3.9) в виде р1 > 0.82 - принимается гипотеза SФМ,
р1 ≤ 0.7 - принимается гипотеза SЧМ,
0,7 < р1 < 0.82 - происходит отказ от принятия решения. Результаты практической проверки определения конкретного вида ФМ-сигнала - ФМ2 или ФМ4 по правилу (3.3.11) при правильном принятии решения о приеме ФМ-сигнала показали вероятность правильного различения ФМ2- и ФМ4-сигналов в диапазоне 0,95...0,98. Рассмотрим возможности определения параметров и вида модуляции сигналов на основе обработки значений мгновенной частоты сигнала, вычисляемой по формуле 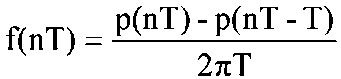
где р(nТ) - абсолютное значение фазы сигнала. Для примера ограничим возможные значения мгновенной частоты значениями от fmin = 500 Гц до fmах = 3500 Гц. Для данного диапазона частот вычисляется гистограмма значений мгновенной частоты ni, i = 1, ...,I. Целью анализа полученной гистограммы является как определение центральной частоты сигнала, так и формирование дополнительных признаков распознавания вида и параметров его модуляции. Для улучшения разделимости отдельных пиков гистограммы, соответствующих различным типам модуляции, гистограмму необходимо подвергнуть специальной обработке. Строится нормированная гистограмма со значениями 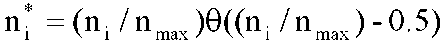
где i = 1,..., I,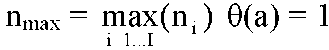 , если a > 0, и , если a > 0, и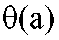 = 0 в противном случае. = 0 в противном случае. По полученной гистограмме определяются минимальное и максимальное ненулевые значения fmin и fmах. Для всех значений f(nT) ∈ [fmin , fmах ] строится оценка функции плотности вероятности ŵf(x) по формуле (3.3.6) при значениях h = 5 и k0 = 3. Особенность определения параметров распределения мгновенной частоты для ЧМ-и ФМ-сигналов заключается в необходимости выделения M вероятных центров рабочих частот (мод - для оцениваемой функции ŵf(x)), причем точное значение M априорно неизвестно. Данная задача может быть решена следующим образом. Предположим, что величина f характеризуется функцией плотности вероятности 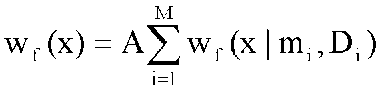 , (3.3.12) , (3.3.12)
представляющей собой смесь M функций нормального свойства с математическими ожиданиями и дисперсиями mi и Di. Пусть wt(x|mt, Dt), называемая испытательной функцией, является нормальной плотностью вероятности с математическими ожиданиями и дисперсиями mi и Di. Рассмотрим возможности оценки математического ожидания и дисперсии j-гo слагаемого выражения (3.3.12). Если wf(x|mj, Dj) является доминантным кластером для испытательной функции вблизи точки х8, тогда 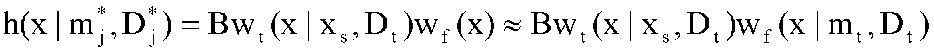
В этом случае в соответствии с [37] 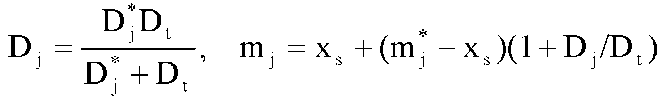 . (3.3.13) . (3.3.13)
В соответствии с полученными выражениями проводятся следующие действия. Производится преобразование функции, где ŵf(xsk) → ŵf(xsk) = msk, где mjk - математические ожидания, вычисленные по формулам (3.3.13) применительно к функции ŵf(x) в точках xsk = fmin + kh, k = 0,...,[(fmax - fmin)/h]. После этого определяются все значения k, для которых функция ŵf(xsk) достигает максимума. Следует отметить, что в ряде практических задач в качестве испытательной функции целесообразно использовать дельту-функцию, что сводит рассматриваемую задачу к задаче поиска Экстремумов функции ŵf(x) стандартными методами. Пусть fj, j = 1,..., M, обозначает ординату j-го наибольшего значения функции ŵf(xsk). На первом этапе выявляется ряд наибольших значений, для которых fj+1 - fi ≥ 40 Гц, что соответствует минимально возможному значению разноса частот. Значение М будет зависеть от вида и параметров модуляции. Так, при M = 2 выявленных пиков полигона может быть принято решение об обнаружении ЧМ2-сигнала. К значению M = 2 в некоторых случаях вследствие сильной корреляционной зависимости параметров мгновенных частоты и фазы может приводить и прием ФМ2- или ФМ4-сигналов, причем значение M = 1 или M = 2 для них часто зависит от вида модулирующего сигнала. Следует отметить, что анализ мгновенной частоты ФМ4-сигнала со скоростью манипуляции V ≥ 600 Бод может в зависимости от используемого режима передачи приводить и к появлению трех или четырех максимумов в гистограмме значений частоты, но обработка гистограммы описанным выше методом приводит к одно- или двухмодальному характеру функции ŵf(xsk). Можно предположить наличие частот fj, для которых значения попарных разностей fj - fi при j > i будут приблизительно равны ΔF, 2ΔF, 3ΔF и т. д., где ΔF - некоторая постоянная величина. Очевидно, что значение ΔF будет являться оценкой разноса частот, а количество максимумов M - оценкой количества частотных позиций сигнала. Для целей дальнейшего анализа необходимо знать разброс возможных оценок ΔF при характерных для канала приема значениях отношения сигнал/шум. Данный разброс определяется дисперсией оценки мгновенной частоты для ЧМ- и ФМ-сигналов. Теоретически при любом отношении сигнал/шум без учета погрешности самого измерителя можно задаться нижней границей оценки Рао-Крамера дисперсии измерения мгновенной частоты гармонического колебания при нормальном шуме [36]. Данная оценка определяется выражением 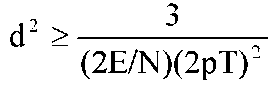 , (3.3.14) , (3.3.14)
где E/N - отношение энергии сигнала к энергии шума, T - время наблюдения. Полное равенство в выражении (3.3.14) возможно только при отсутствии корреляции анализируемого сигнала и сопутствующего шума. Хотя после прохождения сигнала и шума через селективный тракт радиоприемника и фильтр основной селекции демодулятора нельзя говорить о полной их независимости, идеализируя, при дальнейшем обсуждении с целью получения конкретных оценок дисперсии допустим их некоррелированность. В тоже время примем 2E/N = 1 как наименее благоприятный при анализе случай. Таким образом, значение d2 будет целиком определяться временем наблюдения. Отметим, что функция плотности распределении мгновенной частоты f имеет характер нормального закона [38]. При накоплении N = 4096 значений мгновенной частоты f при fd = 10 кГц согласно (3.3.14)d2 ≈ 1,81. Тогда по известному правилу «трех сигм» теоретически возможное значение измерения f будет лежать в интервале от f0 = -4,04 Гц до f0 = +4,04 Гц, где f0 - истинное значение измеряемой частоты. Естественно, данный интервал возможных значений f относится только для немодулированной несущей. При модулированном сигнале величина d2 вследствие изменения значения модуляционного параметра должна быть больше. Если предположить, что переходные процессы модулированного сигнала составляют до 10% от времени измерения, то 90% измерений при общем числе измерений N = 4096 для сигнала любого вида уменьшают дисперсию оценки единичного измерения мгновенной частоты в 4096 — 4096/10 раз, а 10% измерений увеличивают дисперсию оценки в 4096 — 4096*9/10 раз (наименее благоприятный исход). В этом случае по правилу «трех сигм» возможное значение измерения f должно лежать в интервале от f0 = -4,5 Гц до f0 = +4,5 Гц или, округляя с учетом погрешности метода измерения, в интервале от f0 = -5 Гц до f0 = +5 Гц. в 4096 — 4096/10 раз, а 10% измерений увеличивают дисперсию оценки в 4096 — 4096*9/10 раз (наименее благоприятный исход). В этом случае по правилу «трех сигм» возможное значение измерения f должно лежать в интервале от f0 = -4,5 Гц до f0 = +4,5 Гц или, округляя с учетом погрешности метода измерения, в интервале от f0 = -5 Гц до f0 = +5 Гц. Таким образом, при выявлении M наибольших значений функции ŵf(x) для которых М ∈ [4, 6, 8, 12, 13, 16] и справедливо выражение fj+1-fj = ΔḞ±5 Гц, где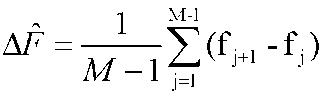 , можно предположить наличие многопозиционного ЧМ- сигнала с числом позиций M и разносом частот ΔF. Центральная частота сигнала fц определяется из выражения , можно предположить наличие многопозиционного ЧМ- сигнала с числом позиций M и разносом частот ΔF. Центральная частота сигнала fц определяется из выражения 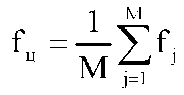
При наличии в оценке ŵf(x) только двух пиков (M = 2) можно полагать о приеме сигнала ЧМ2, либо сигналов ФМ2 или ФМ4. В этом случае окончательное решение может быть принято на основе обработки значений мгновенной фазы сигнала по методам, описанным выше. Однако результаты экспериментов по обработке сигналов с ФМ2 и ФМ4 показали, что наиболее часто двухмодальный характер функции ŵf(x) при выбранном номинале fd = 10 кГц имеет место при скоростях манипуляции свыше 300 Бод, модулирующем сигнале типа меандр и выполнении условий f2-f1>200 Гц и ŵf(f1)/ŵf(f2) (3.4.15) Нарушение даже одного из неравенств свидетельствует о приеме сигнала ЧМ2. По этой причине эмпирическое правило (3.4.15) может быть использовано в процедурах различения сигналов ФМ и ЧМ. Наличие в оценке ŵf(x) только одного максимума свидетельствует либо о приеме ФМ-сигнала, либо о наличии немодулированного колебания, часто применяемого в практике радиосвязи, например, для обозначения занятости радиочастоты. Очевидным способом разрешения данной ситуации является применение решающего правила (3.3.9). Потенциальная теоретически достижимая вероятность ошибки определения вида модуляции на основе контроля только мгновенной частоты при различных соотношениях сигнал/шум равна потенциальной достижимой вероятности при контроле фазы. Проведенная проверка в реальных условиях приема КВ-радио-каналов эффективности разработанных методик распознавания фазоманипулированных и частотноманипулированных сигналов показала их работоспособность в условиях низкого отношения сигнал/шум. Сравнительно невысокие по сравнению с другими методами вычислительные затраты на реализацию описанных методов создают реальные предпосылки для их использования при синтезе различных средств цифровой обработки радиосигналов при неполном априорном знании о точном значении их параметров. На рис. 3.3.3 представлен один из вариантов алгоритма определения вида и параметров модуляции сигналов с постоянной огибающей со скоростями до 1200 Бод. 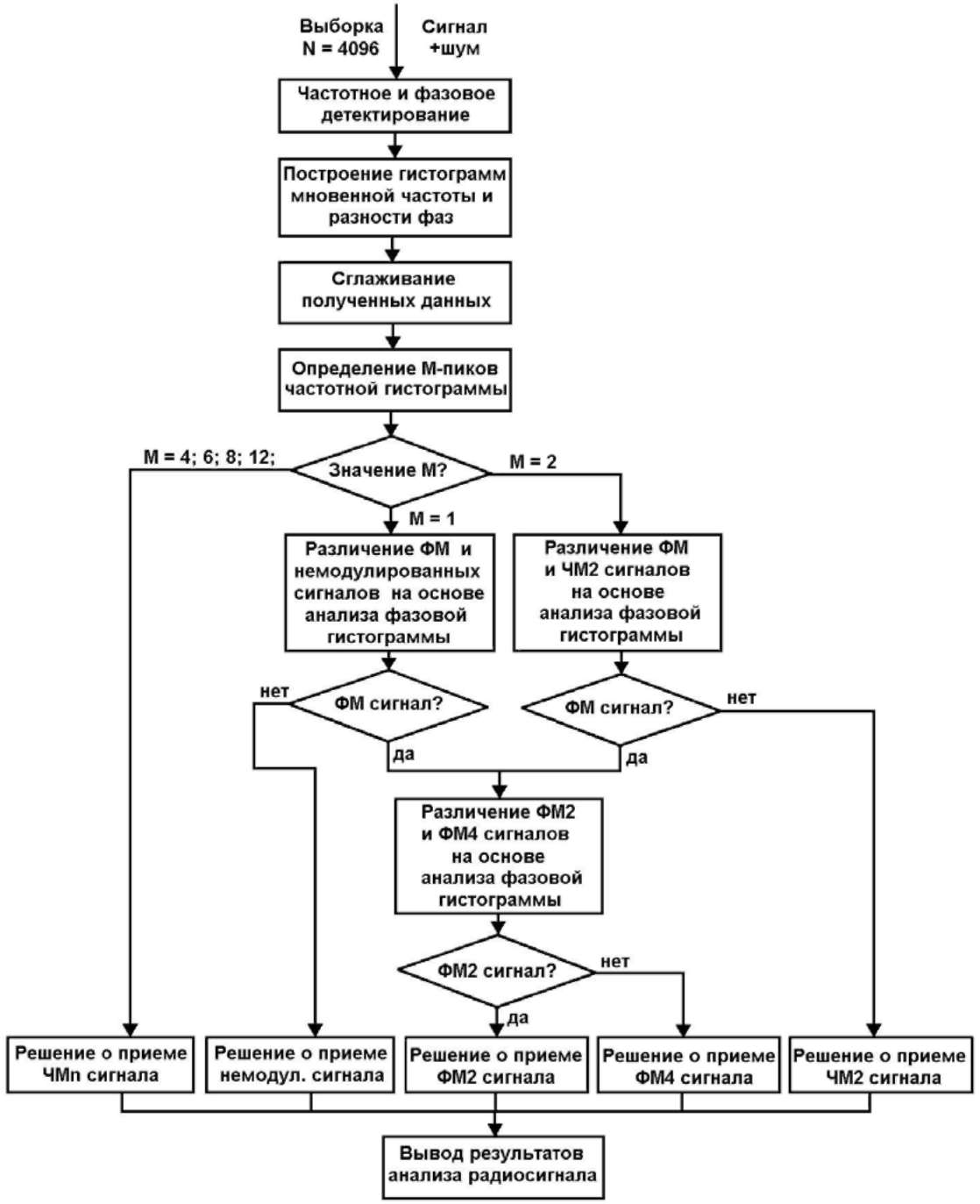
Рис. 3.3.3 Подводя итог сказанному о методах автоматического определения вида и параметров модуляции можно сделать следующие выводы.
- Для проведения технического анализа модуляционной структуры сигналов систем радиосвязи использование классических методов оптимальной оценки параметров и статистической теории распознавания образов малоэффективно. Требование оперативности настройки обрабатывающей аппаратуры обусловливает необходимость разработки специальных методов определения модуляционных параметров по неклассифицированной выборке фиксированного объема.
- Используемая при распознавании вида и параметров модуляции обработка выборки мгновенных значений сигнала осуществляется с целью получения оценок суммарных М-модальных распределений значений мгновенных частоты и фазы сигнала, образованных М нормальными слабо пересекающимися частными распределениями. При этом элементы данных распределений отображают значения несущей частоты, фазовых сдвигов для сигналов с ФМ, частотных позиций для ЧМ-сигналов.
- Используемые в рассмотренных процедурах определения вида и параметров модуляции методы выделения характерных особенностей для ФМ2-, ФМ4- и ЧМ2...16- сигналов позволяют максимально сократить требуемый объем априорных знаний об анализируемом сигнале.
Список литературы: - Трифонов А. П., Шинаков Ю. С. Совместное различение сигналов и оценка их параметров на фоне шумов. - М.: Радио и связь, 1986.
- Фомин Я. А., Тарловский Г. Р. Статистическая теория распознавания образов. - М.: Радио и связь, 1986.
- Дуда P., Xapm П. Распознавание образов и анализ сцен. - М.: Мир, 1976.
- Тихонов В. И. Оптимальный прием сигналов. - М.: Радио и связь, 1983.
- Левин Б. Р. Теоретические основы статистической радиотехники. Книга 1. - М: Сов. Радио, 1974.
- Френке Л. Теория сигналов. - М.: Сов. Радио, 1974.
|